Lab 4: Base R data exploration
🧑💻 Make sure to finish previous labs before continuing with this one! It might be tempting to skip some stuff if you’re behind, but you may just end up progressively more lost … we will happily answer questions from any lab each week 😃
5.4 Diamonds 💎 data
You have now seen some data comes built into R, or an add-on package to R, because it is useful for learning or experimenting. We will use one such data set which is of a decent size so that it becomes clear you can’t just sift through many data sets, you really do need the tools we’ve learned in the lecture practicals to answer interesting questions.
Exercise 5.31 We will install, load and read about the diamonds data:
- Install the package
ggplot2from CRAN - Load the
diamondsdata from theggplot2package - Look at the help file for this data to learn a little about what variables were collected.
Click for solution
## SOLUTION i.
install.packages("ggplot2")## SOLUTION ii.
data("diamonds", package = "ggplot2")## SOLUTION iii.
# If the ggplot2 package is not loaded, you need to use the full reference to
# the dataset in the form 'package::data'
?ggplot2::diamonds
# If the package is loaded, you can use the short form
?diamonds
We will use this data to do a series of quick-fire exercises, then a few that you may need a little longer to figure out.
You should not need to write lots of code to answer these questions if you are using the methods from the course so far.
Exercise 5.32 How many observations and how many variables are there in the data?
Click for solution
## SOLUTION
# Number of observations (recall: observations in rows)
nrow(diamonds)[1] 53940# Number of variables (recall: variables in columns)
ncol(diamonds)[1] 10# Or, you might have chosen to just show the dimensions and get both at once
dim(diamonds)[1] 53940 10Exercise 5.33 How many factor type variables are there?
Click for solution
Remember from lectures that factors are categorical data types, which are handled quite differently from numeric data.
There are a few ways to answer this … perhaps the simplest is to use our good friend str() to examine the structure of the data set:
## SOLUTION
str(diamonds)tibble [53,940 × 10] (S3: tbl_df/tbl/data.frame)
$ carat : num [1:53940] 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ...
$ cut : Ord.factor w/ 5 levels "Fair"<"Good"<..: 5 4 2 4 2 3 3 3 1 3 ...
$ color : Ord.factor w/ 7 levels "D"<"E"<"F"<"G"<..: 2 2 2 6 7 7 6 5 2 5 ...
$ clarity: Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 2 3 5 4 2 6 7 3 4 5 ...
$ depth : num [1:53940] 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ...
$ table : num [1:53940] 55 61 65 58 58 57 57 55 61 61 ...
$ price : int [1:53940] 326 326 327 334 335 336 336 337 337 338 ...
$ x : num [1:53940] 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ...
$ y : num [1:53940] 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ...
$ z : num [1:53940] 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...Exercise 5.34 Print just the first few observations in the data.
Click for solution
## SOLUTION
head(diamonds)# A tibble: 6 × 10
carat cut color clarity depth table price x y z
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
4 0.29 Premium I VS2 62.4 58 334 4.2 4.23 2.63
5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48# Or, the above shows 6 rows by default, add a number to change how many to
# peek at, eg
head(diamonds, 10)# A tibble: 10 × 10
carat cut color clarity depth table price x y z
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
4 0.29 Premium I VS2 62.4 58 334 4.2 4.23 2.63
5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
7 0.24 Very Good I VVS1 62.3 57 336 3.95 3.98 2.47
8 0.26 Very Good H SI1 61.9 55 337 4.07 4.11 2.53
9 0.22 Fair E VS2 65.1 61 337 3.87 3.78 2.49
10 0.23 Very Good H VS1 59.4 61 338 4 4.05 2.39Exercise 5.35 What are the summary statistics (eg min/max, mean, median, counts, …) for each variable?
Click for solution
## SOLUTION
summary(diamonds) carat cut color clarity depth
Min. :0.2000 Fair : 1610 D: 6775 SI1 :13065 Min. :43.00
1st Qu.:0.4000 Good : 4906 E: 9797 VS2 :12258 1st Qu.:61.00
Median :0.7000 Very Good:12082 F: 9542 SI2 : 9194 Median :61.80
Mean :0.7979 Premium :13791 G:11292 VS1 : 8171 Mean :61.75
3rd Qu.:1.0400 Ideal :21551 H: 8304 VVS2 : 5066 3rd Qu.:62.50
Max. :5.0100 I: 5422 VVS1 : 3655 Max. :79.00
J: 2808 (Other): 2531
table price x y
Min. :43.00 Min. : 326 Min. : 0.000 Min. : 0.000
1st Qu.:56.00 1st Qu.: 950 1st Qu.: 4.710 1st Qu.: 4.720
Median :57.00 Median : 2401 Median : 5.700 Median : 5.710
Mean :57.46 Mean : 3933 Mean : 5.731 Mean : 5.735
3rd Qu.:59.00 3rd Qu.: 5324 3rd Qu.: 6.540 3rd Qu.: 6.540
Max. :95.00 Max. :18823 Max. :10.740 Max. :58.900
z
Min. : 0.000
1st Qu.: 2.910
Median : 3.530
Mean : 3.539
3rd Qu.: 4.040
Max. :31.800
summary() has been sensible and just given us counts for the factor variables.
Exercise 5.36 Find the total value of all ideal cut diamonds, with colour code D and with depth percentage of 60 or less.
Is that total value greater or less than $200,000?
Click for solution
## SOLUTION
sum(diamonds[diamonds$cut == "Ideal" & diamonds$color == "D" & diamonds$depth <= 60,"price"])[1] 196479Exercise 5.37 Create a new variable named ppc in the diamonds data frame which contains the price per carat of each diamond. Then compute the overall median price per carat.
Click for solution
## SOLUTION
diamonds$ppc <- diamonds$price / diamonds$carat
median(diamonds$ppc)[1] 3495.198Exercise 5.38 Plot a simple scatterplot of caret on the x-axis and ppc on the y-axis. (Note: this is a bigger dataset, so this plot might take a few seconds to display after you run the function)
Click for solution
## SOLUTION
plot(diamonds$carat, diamonds$ppc)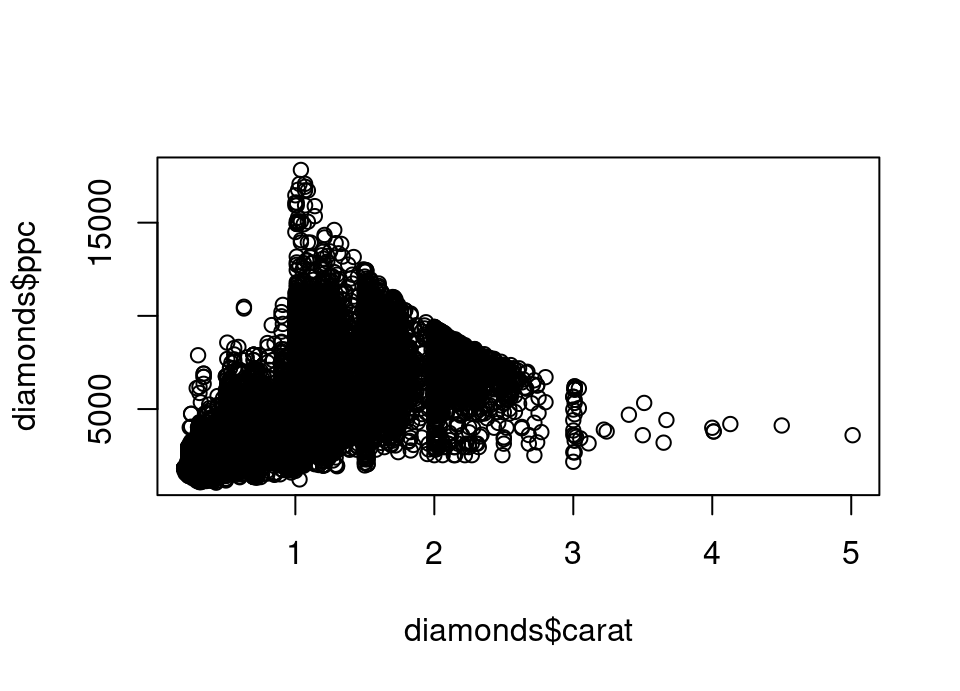
We can add horizontal or vertical lines to our plots with the abline() function. For example, if you run abline(v = 1) it will add a vertical line which crosses the x-axis at 1. If you run abline(h = 1000) it will add a horizontal line which crosses the y-axis at 1000.
Exercise 5.39 We will add some visual guides to help us:
- add a horizontal line to your plot at the mean price per carat
- add vertical lines at carat equals 1, 2, 3, 4 and 5
- Using these visual guides, roughly what range of carats seem to attract the highest price per carat?
Click for solution
## SOLUTION
plot(diamonds$carat, diamonds$ppc)
abline(h = mean(diamonds$ppc))
abline(v = 1:5)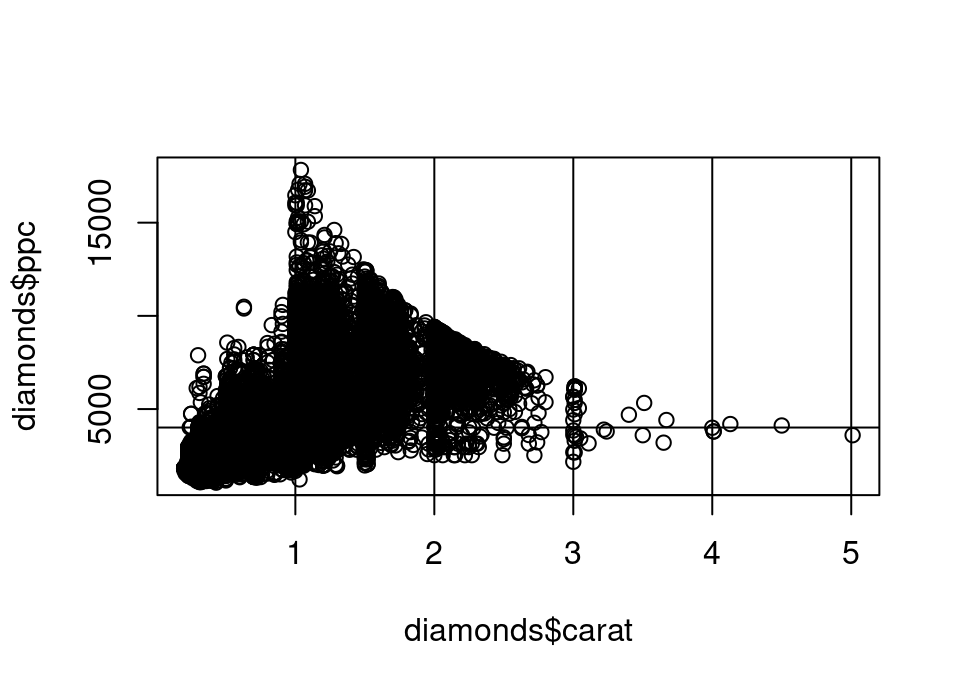
- It looks like many diamonds between 1 and 2 carats attract a large premium in the price you pay per carat.
- Indeed, there is something of a cliff edge effect at the 1 carat value. Can you speculate why?
- This is somewhat, but less, in evidence between 2 and 3 carats: in this case the spread above the mean is not so exaggerated compared to the spread below the mean.
- Across all carat levels there is a lot of spread though, so within all ranges there are some diamonds which are very average in the price per carat.
Exercise 5.40 Create two new data frames. Both should contain only the diamonds whose carat is between 1 and 2 and:
- the first should have
ppcexceeding 10000 - the second should have
ppcless than or equal to 10000
Using these data frames, provide counts of the clarity variable for each data frame. Is there a clear difference?
Click for solution
## SOLUTION
high.ppc <- diamonds[diamonds$ppc>10000 & diamonds$carat >= 1 & diamonds$carat < 2,]
normal.ppc <- diamonds[diamonds$ppc<=10000 & diamonds$carat >= 1 & diamonds$carat < 2,]
table(high.ppc$clarity)
I1 SI2 SI1 VS2 VS1 VVS2 VVS1 IF
0 0 0 77 115 167 144 110 table(normal.ppc$clarity)
I1 SI2 SI1 VS2 VS1 VVS2 VVS1 IF
415 4220 4511 3641 2179 901 286 140 According to the documentation we saw at the start of the lab, clarity is a measurement of how clear the diamond is (I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best))
Clearly the high price per carat diamonds contain only diamonds of clarity VS2 or better. The vast majority of normal price per carat diamonds are of clarity VS1 or worse. So clarity is perhaps one factor contributing to the excessive price per carat of diamonds in this carat range.Exercise 5.41 What is the price, number of carats, cut and clarity of the most expensive diamond in the data?
Click for solution
## SOLUTION
pricy <- diamonds[order(diamonds$price, decreasing = TRUE)[1], c("price", "carat", "cut", "clarity")]
pricy# A tibble: 1 × 4
price carat cut clarity
<int> <dbl> <ord> <ord>
1 18823 2.29 Premium VS2 To help understand the above, break it down:
order(diamonds$price)provides the row numbers from lowest to highest priceorder(diamonds$price, decreasing = TRUE)switches this to highest to lowest priceorder(diamonds$price, decreasing = TRUE)[1]gets just the first element, in other words the row number of the highest priced diamond- The above is passed as the row value in the
[ , ]and the vector of column names is provided in the column values.
Exercise 5.42 Are there any diamonds in the data which have more carats, superior cut and superior clarity than the most expensive diamond? What is the biggest saving you could make if you just wanted to improve on these characteristics versus the most expensive diamond?
Click for solution
## SOLUTION
# Yes, the following has more than zero rows, so there are cheaper diamonds
# which are better on all those characteristics
improve <- diamonds[diamonds$carat > pricy$carat & diamonds$cut > pricy$cut & diamonds$clarity > pricy$clarity,]
improve# A tibble: 4 × 11
carat cut color clarity depth table price x y z ppc
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl>
1 2.59 Ideal J VS1 61.7 56 16465 8.83 8.77 5.43 6357.
2 2.39 Ideal J VS1 62.1 57 17365 8.53 8.57 5.31 7266.
3 2.36 Ideal J VS1 61.6 57 17829 8.6 8.55 5.28 7555.
4 2.32 Ideal J VS1 62.5 54.5 17891 8.44 8.47 5.28 7712.# Potential saving is:
pricy$price - min(improve$price)[1] 2358🏁🏁 Done, end of lab! 🏁🏁