Reliability Theory
Supervisors*: Dr L.J.M. Aslett and Prof F.P.A. Coolen
Reliability theory tries to assess our uncertainty in whether machines and other systems will function correctly. It uses probability and statistics to estimate the chances of a part or a whole system failing. Reliability theory is mostly used for engineered systems, though it is related to biological survival analysis, like studying how long a person will live. When we talk about engineered systems, we focus on the reliability of all the parts that make it up, while in contrast for biological systems we typically look at individual 'units', like people.
The origins of modern reliability theory can be traced to World War II and the advent of complex military systems whose failure characteristics had to be well understood. A fascinating historical exposition of some of this pioneering work following its declassification is in Mangel and Samaniego (1984).
Consider the following so-called reliability block diagram:
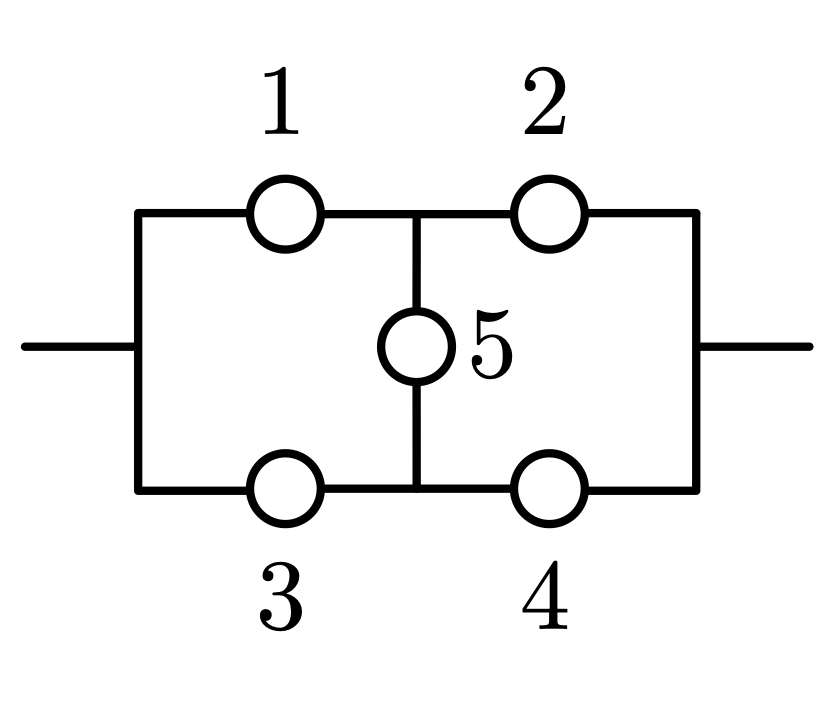
The whole diagram represents a system, whilst each circle denotes a numbered 'component' in that system. The system as a whole is considered to be functional if there is a route from the left most input line through to the right most exit line which passes only through components which are themselves functional. The probability that the system is functional is the probability that there is such a path through the diagram. For example, in this system, if only components 1 and 2 have failed, the system will function since there is a path via the functional components 3 and 4. Likewise, if only components 1 and 4 have failed, there is a path via 3, 5 and 2. However, should components 1, 4 and 5 (or more) fail then the system fails.
The ability for the system to operate in terms of functional components can therefore be characterised by the 'path sets' \( \{1,2\}, \{3,4\}, \{1,4,5\}, \{2,3,5\} \), or in a complementary manner it's inability to operate by the 'cut sets' \( \{1,3\}, \{2,4\}, \{1,4,5\}, \{2,3,5\} \). At the simplest level we can consider a fixed probability that each component functions, but in this project we will be interested in the more advanced view where we have lifetime probability distributions for each component (and in the even more advanced setting, we may incorporate a repair process with associated distribution). We can use the basic cut/path set characterisation to construct gradually more sophisticated ways to express the operational status of a system, via structure function (Birnbaum et al., 1961), system signatures (Samaniego, 1985), and survival signatures (Coolen and Coolen-Maturi, 2012).
There are many directions in which this can be taken, depending on the interests of the student. This can include probabilistic questions of optimal design, statistical inference in both parametric and non-parametric settings (Aslett et al., 2014), reliability of complex system missions (Huang et al., 2019), analysis of repairable systems by treatment as a stochastic process, and many more.
*Dr Aslett will supervise Michaelmas and Prof Coolen will supervise Epiphany.
Prerequisites
Statistical Inference II and Probability I.
References
Aslett, L.J.M., Coolen, F.P.A. and Wilson, S.P., 2015. Bayesian inference for reliability of systems and networks using the survival signature. Risk Analysis, 35(9), pp.1640-1651. DOI: 10.1111/risa.12228
Birnbaum, Z.W., Esary, J.D. and Saunders, S.C., 1961. Multi-component systems and structures and their reliability. Technometrics, 3(1), pp.55-77. DOI: 10.1080/00401706.1961.10489927
Coolen, F.P.A. and Coolen-Maturi, T., 2012. Generalizing the signature to systems with multiple types of components. In Complex Systems and Dependability (pp. 115-130). Springer Berlin Heidelberg. DOI: 10.1007/978-3-642-30662-4_8
Huang, X., Aslett, L.J.M. and Coolen, F.P.A., 2019. Reliability analysis of general phased mission systems with a new survival signature. Reliability Engineering & System Safety, 189, pp.416-422. DOI: 10.1016/j.ress.2019.04.019
Mangel, M. and Samaniego, F.J., 1984. Abraham Wald's Work on Aircraft Survivability. Journal of the American Statistical Association, 79(386), pp.259-267. DOI: 10.2307/2288257
Samaniego, F.J., 1985. On closure of the IFR class under formation of coherent systems. IEEE Transactions on Reliability, 34(1), pp.69-72. DOI: 10.1109/TR.1985.5221935