Hidden Markov Models
Supervisors: Dr L.J.M. Aslett & Prof P.S. Craig
In many scientific problems, the object of interest cannot be directly observed or measured. The Hidden Markov Model (HMM) is a flexible class of models which can be used to address a large range of such problems, formalising how to learn about the latent feature of interest given indirect (often noisy) observations. In sophisticated applications, HMMs often form a crucial component in a larger analysis, incorporating supervised and unsupervised learning methods.
The model considers a sequence of latent random variables, \( X_t \), which give rise to a sequence of observable random variables, \( Y_t \).
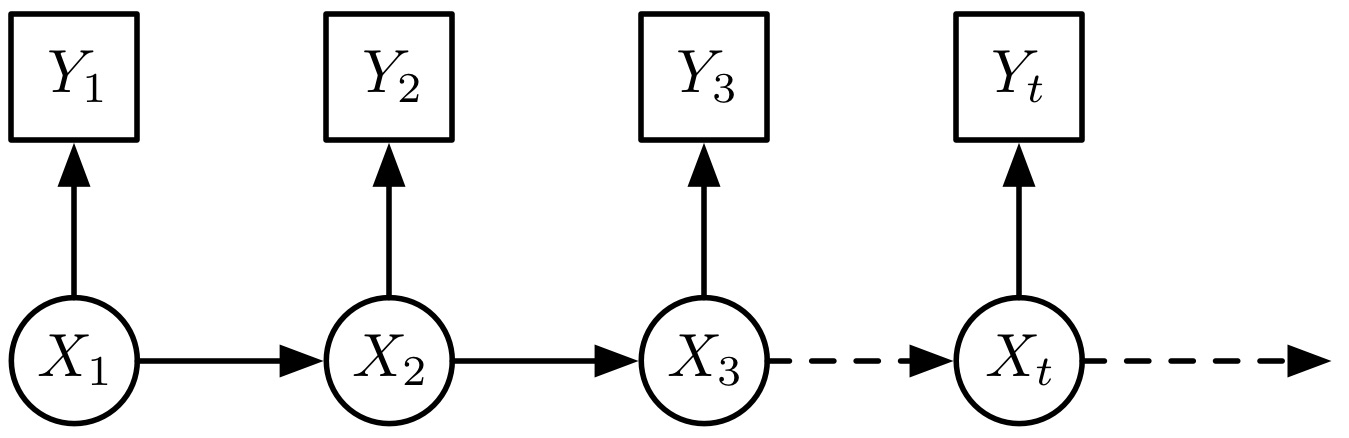
The nomenclature ‘hidden’ arises from the fact that interest is usually (at least in part) in the \( X_t \)’s, yet data is typically only available for the \( Y_t \)’s; whilst ‘Markov’ expresses the assumption that the \( X_t \) have only a sequential dependence structure. There are many potential choices to model the latent state transitions, \( \mathbb{P}(X_{t+1} | X_t) \), and observation process, \( \mathbb{P}(Y_t | X_t) \), with a rich literature on performing inference in both classical and Bayesian paradigms.
Example applications which make use of HMMs as a crucial component include speech and handwriting recognition, missile tracking, genome modelling, gesture recognition, changepoint detection, etc. Indeed, HMMs are such a ubiquitous element in modelling of biotechnology problems that they have even been referred to as “… the Legos of computational sequence analysis” (Eddy, 2004).
The goal will be to initially learn dynamic programming and the core HMM forward, backward, Viterbi and Baum-Welch algorithms. With this understanding you may then take the project in whatever direction you find most interesting, which might include: examining Bayesian methods for HMMs; exploring a particular application; combining HMMs with supervised and unsupervised learning algorithms; examining Sequential Monte Carlo methods for HMMs; etc.
Prerequisites
Statistical Concepts II and Statistical Methods III. Familiarity with the statistical language R (or alternatively Python/Julia) is essential.
Optional Modules
Some of the possible directions the project could be taken in would intersect with Bayesian Statistics IV, but it is not corequisite as many other possible directions are available.
Background
Sections I-III of Rabiner (1989) is a good compact tutorial paper on the core material. Ghahramani (2001) is a more extensive tutorial paper with focus on inference in HMMs. There are also books devoted to HMMs, from the accessible (Fraser, 2008) to the more rigorous (Cappé et al., 2005).
References
Cappé, O., Moulines, E. and Rydén, T., 2005. Inference in hidden Markov models. Springer. Durham Library
Eddy, S.R., 2004. What is a hidden Markov model? Nature Biotechnology, 22(10), p.1315. DOI: 10.1038/nbt1004-1315
Fraser, A.M., 2008. Hidden Markov models and dynamical systems. Society for Industrial and Applied Mathematics. Durham Library
Ghahramani, Z., 2001. An introduction to hidden Markov models and Bayesian networks. International Journal of Pattern Recognition and Artificial Intelligence, 15(01), pp.9-42. DOI: 10.1142/S0218001401000836
Rabiner, L.R., 1989. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE, 77(2), pp.257-286. DOI: 10.1109/5.18626